ランチェスター戦略、ランチェスター法則の第二法則（第2法則）強者の戦略／ランチェスター戦略の理論V0l.4
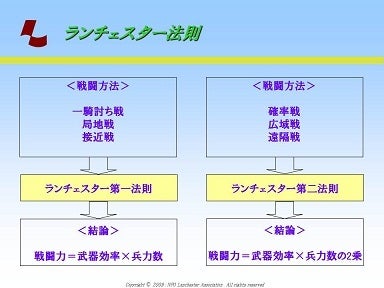
次は第二法則（右側）です。下の図を見てください。
「第二法則（右側）」が適用される戦い方は、
確率戦、広域戦、遠隔戦
・・・です。
確率戦というのは聞き慣れない言葉かもしれませんが、
確率兵器（マシンガンなど複数の敵にダメージを与えられる兵器）
を使った戦い方や団体戦のことだと思ってください。
このような戦い方の時、
戦闘力＝武器効率×兵力数の二乗
・・・となります。
第一法則と違うのは「兵力数の二乗」というところです。
二乗倍と言うのは相当の戦闘力になりますが、
本当に二乗倍の戦闘力になるのでしょうか？
数式を使って検証してみましょう。
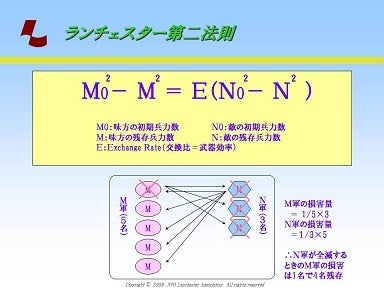
下の図を見てください。
見慣れない公式だと思いますが、
算数のレベルなので難しいことはありません。
第一法則と異なるのは全て二乗倍になっているところです。
第二法則でも第一法則と同様に計算し易くするため
「武器効率」の「Ｅ」を「１」とします。
そうすると・・・
「味方の初期兵力数の二乗」－「味方の残存兵力数の二乗」 ＝「敵の初期兵力数の二乗」－「敵の残存兵力数の二乗」
・・・となります。
ここではマシンガンを持った兵士同士の戦いを
イメージしながら上の図をみてください。
先ず、本当に二乗倍の戦闘力（＝損害量）
となるのか見てみましょう。
第一法則と同様に味方が５人、
敵が３人でどちらかの軍が全滅するまで戦います。
味方が敵から攻撃を受けた場合、当たる確立は１/５です。
１/５の確率で当たる攻撃を敵３人からを受けるので
味方１人の損害量は１/５×３＝３/５となります。
そして敵兵士の場合は１/３の確率で当たる攻撃を
味方５人で攻撃しますから１/３×５＝５/３となります。
味方の損害量が３/５、敵の損害量が５/３、 通分すると
⇒ ９/１５：２５/１５ 分子を比較すると
⇒ ９：２５
これは３の二乗：５の二乗
・・・で敵の数の二乗倍になっていることがわかります。
では敵軍３人が全滅するまで戦うと
図のように味方は４人も残るのでしょうか？
第一法則の時とあまりにも数が異なりますが、
これも実際に数値を代入して検証してみましょう。
上に同じ図を掲載しておきます。
味方の軍の兵士が何人残るのかを検証しているので、
公式の中でも「Ｍ」（味方の残存兵力数）は
そのまま「Ｍ」として使います。
5の二乗－Ｍの二乗＝３の二乗－０の二乗
２５－Ｍの二乗＝９－０ Ｍの二乗＝１６ Ｍ＝４
・・・となり、図の通り
味方の兵士Ｍ軍が４人残って勝つことがわかります。
ではこの第二法則の場合、
敵のＮ軍がＭ軍に勝つには武器効率（Ｅ）の数値を
いくらにすれば良いでしょうか？
Ｎ軍が勝つわけですから不等号を用いて・・・
２５－０＜Ｅ（９－０） ⇒ ２５＜９Ｅ ２５/９＜Ｅ ⇒ ２．７７７・・・
ここで第一法則の時の武器効率（Ｅ）と比べてください。
第一法則の時は１．６７でした。
第二法則では第一法則と同じ兵士の数でも
より大きな武器効率の数値２.７８が必要になります。
従って、二乗倍の戦闘力（損害量）となる第二法則では
Ｎ軍は多少武器効率を上げても勝つことができない、
Ｍ軍は兵力数が多いので多少相手の武器効率が高くても
それを凌駕することができる圧倒的な戦闘力を持つことがわかります。
次はこの第一法則と第二法則を
ビジネスに置き換えると何が言えるのか？
戦争の法則からビジネスの法則にどのように応用するのか？
をお伝えします。
-
経営者必読の書として絶賛された！『儲かる会社88の鉄則』92ページ分を進呈
-
毎月50件の新規受注を獲得する！"ネット集客・Web集客の全体設計図" 120分以上の動画を進呈
-
売上2倍は難しくない！売上アップの方程式と10の打ち手とは？